티스토리 뷰
알고리즘을 풀다보면 fft 로 풀리는 문제가 참 많다.
왜 이런 변환을 사용하게 됐는지, 어떤 문제에서 사용하면 되는지 알아보기위해 영상을 보면서 정리를 해보자
FFT 란 뭘까?
https://www.youtube.com/watch?v=eKSmEPAEr2U
푸리에 변환이란 어떤 신호를 주파수 종류별로 분해하는 방법.
기존 신호에, 사인파, 코사인파를 곱한 면적을 더하는 방식으로 해당 주파수가 얼마나 연관이 있는지 알아낸다.
신호가 여러 주파수의 합으로 구성된 경우, 어떤 주파수가 존재하고 어느 비율로 존재하는지 알수 있게됨.
사인파와 코사인파의 진폭을 계산할때 오일러 공식을 사용하여, 하나의 지수항으로 계산이 가능
실수부는 코사인파의 진폭, 허수부는 사인파의 진폭
그러나 실제로 얻는 신호는, 무한한 연속파가 아니고, 유한하며 하나하나의 포인트로 이루어짐
데이터는 이산적이고 유한할 수 밖에 없음
따라서 DFT 이산 푸리에 변환을 사용
DFT 는 측정하는 주파수 또한 이산적임.
신호의 샘플 간격이 넓을수록 고 주파수는 측정 할 수 없음
신호의 샘플 간격이 짧을 수록 유사한 주파수를 구분짓기 어려워짐.
이산적으로 간다면 포인트가 8개 있을때
0 : offset (포인트의 합)
n (1~7) : sin, cos 의 주파수를 n hz 으로 잡고 곱한 값의 합
그러나 너무 많은 계산이 필요함 (N^2)
Fast Fourier Transform 으로 시간을 단축
정형파의 주기적 특성 : 서로다른 주파수의 파동들은 특정 지점에서 겹치게됨 (N 대신 logN 을 사용)
짝수번째, 홀수번째 포인트로 나눔.
0~3 번째 주파수와 4~7 번째 주파수를 비교
짝수번째 : 두 사인파의 값이 동일 / 홀수번째 : 두 사인파의 값이 하나의 음수값임
이를 끝까지 겹쳐서 사용하면 N logN 이됨
우리가 푸는 알고리즘에서의 FFT 는 뭘까?
그러면 실제 문제를 풀면서 알아보자. 코드는 다른분들 코드로 가져오는데, 내가 이해를 해야한다
https://www.acmicpc.net/problem/15576
https://web.cecs.pdx.edu/~maier/cs584/Lectures/lect07b-11-MG.pdf
1.
다항식 y = aₙ xⁿ + aₙ₋₁ xⁿ⁻¹ + ... a₁ x + a₀ 에 대해
계수 표현식은 계수를 0부터 n 까지 나타낸 것 (a0 .. an)
2.
Horner’s rule 에 의해 y 를 구하는 것은 O(n) 에 가능
3.
계수 표현식의 n 이었다면 A(x) * B(x) 인 C(x) 는 (c0 .. a 2n -1) 로 나옴
A(x) = a3 x^3 + a2 x^2 + a1 x + a0 -> 계수 표현식 (a0, a1, a2, a3)
B(x) = b3 x^3 + b2 x^2 + b1 x + b0 -> 계수 표현식 (b0, b1, b2, b3)
C(x) = a3b3 x^6 + (a3b2 + a2b3) x^5 + (a3b1 + a2b2 + a1b3) x^4 + ...
사실 이 표현은 convolution 과 동일
convolution : 하나의 함수와 또 다른 함수를 반전 이동한 값을 곱한 다음 구간에 대해 적분하여 새로운 함수를 구하는 수학
계수 표현식을 벡터처럼 보면
[a0, a1, a2, a3] / [b0, b1, b2, b3]
C[0] = a[0] * b[0]
C[1] = a[0] * b[1] + a[1] * b[0]
C[2] = a[0] * b[2] + a[1] * b[1] + a[2] * b[0]
C[3] = a[0] * b[3] + a[1] * b[2] + a[2] * b[1] + a[3] * b[0]
C[4] ..
C[5] ..
C[6] = a[0] * b[6] + a[1] * b[5] + a[2] * b[4] + a[3] * b[3] + a[4] * b[2] + a[5] * b[1] + a[6] * b[0] = a[3] * b[3]
따라서 다항식의 곱은 convolution 과 동일하다고 볼수 있음
4.
Point-Value Representationn 차 방정식을 n개의 x, y 쌍으로 나타낸 표현식A(x) = x^3 - 2x + 1 일때{(0,1), (1,0), (2,5), (3,22)}이 Point-Value Representation 을 구할때는 x 하나마다, n 의 계산이 들기때문에, n 개의 값을 구할때 O(n^2) 가 소요됨
5.Point-Value Representation 을 n 개 가지고 있을때, 역으로 n 차 방정식을 만들때 O(n^2) 가 소요됨 Lagrange's formula
6.Point-Value Representation 의 합은 O(n). 그야 y 값만 더하면 되니까
7.만약 Polynomial 을 곱한 Point-Value 를 원한다면, 곱해진 다항식의 차수만큼 포인트가 필요함.따라서 n 차 방정식을 곱한다면 Point 는 2n - 1 이 되어야함 O(n)ex) {(-3, y) ... (0, y') ... (3, y'')}
8.그러면 대체 왜 1~7 을 설명했냐. 왜냐면 다항식을 곱한 coefficient 를 쌩으로 구하면 O(n^2) 인데, 이걸 다른 방법으로 해보고자 했음. 그러나 여전히 O(n^2) 인데 여기서 줄일수 있는걸 줄여보자임
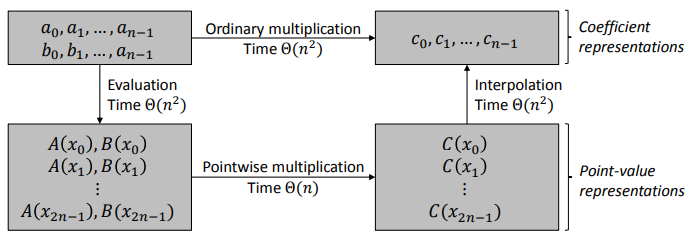
그러면 이걸 어떻게 FFT 를 적용시킬껀데?
1. A(x) 랑 B(x) 를 2^n 벡터로 변경
2. FFT 로 A,B 를 계산 O(nlogn)
3. Point-Value Representation 으로 곱 O(n)
4. Inverse 로 곱한걸 다시 변환하면 C 로 변경
FFT 를 구하기 전에 필요한 사전지식Complex Roots of Unity (복소수 단위근)복소수 중 n 제곱을 하면 1이되는 수들을 의미함. complex 𝒏 th root of unity
𝜔ⁿ = 1
이때 𝜔 는 항상 n개의 해를 가짐. 이들을 단위근이라 부름
z ⁿ −1=0
(z−1)(z−ω)…(z−ω ⁿ −1)=0
이때 𝜔 는 𝑒^(2𝜋𝑖𝑘/n) for k = 0, 1, ... n - 1 이 됨. 이 공식은 복소수를 극 형식으로 나타낸후 n 승을 취했을때 1이 나오는 지점을 구하면서 도출 됨
이때 𝜔 ₙ = e^ (2𝜋𝑖/n) 는 기본 단위근이 되서 단위 원을 n 등분 하는 각 중 첫번 째 회전각을 가지는 복소수
그리고 𝒏 th root of unity 는 𝜔ₙ 의 거듭 제곱으로 표현이 가능
그리고 이 𝜔ₙ 을 A( 𝜔ₙ^k ) 로 넣었을때
짝수부 A[0](x) = a0 + a2x^2 + a4x^4 ..
홀수부 A[1](x) = a1x + a3x^3 + a5x^5
가 되는데, 𝜔ₙ = ( 𝜔₂ₙ)² 이기 때문에 -> 왜냐하면 회전 변환이기 때문이다
A(x) = A[0](x²)+ xA[1](x²) 가 된다
코드에 주석을 달아보자
// cos 와 sin 을 한번에 계산하기 위해 복소수를 사용 (오일러 공식: e^(ix) = cos(x) + i*sin(x))
typedef complex<double> cpx;
// 이산 신호가 a 로 들어왔을 때, 각 주파수별 cos 파, sin 파와 곱한 값을 구할 것
void fft(vector<cpx>& a, bool inv = false) {
// 계속 반으로 접을 것 이기 때문에 n 이 2^n 로 만들고 들어오게됨
int n = a.size(), j = 0;
// 비트 반전 정렬 (Bit Reversal Permutation)
// 짝수번째를 몰고, 홀수번째를 모는건 알겠는데,
// 이 비트반전 정렬은 왜 필요하며,
// 왜 이렇게 구현된걸까?
// -> 다니엘슨-란초스 보조정리
// 이렇게 정렬을 해두면 다음번에 다시 반으로 쪼갤 때 이미 나눠져 있다
// | n | binary | reverse | reverse dec |
// | 0 | 000 | 000 | 0 |
// | 1 | 001 | 100 | 4 |
// | 2 | 010 | 010 | 2 |
// | 3 | 011 | 110 | 6 |
// | 4 | 100 | 001 | 1 |
// | 5 | 101 | 101 | 5 |
// | 6 | 110 | 011 | 3 |
// | 7 | 111 | 111 | 7 |
for (int i = 1; i < n; i++) {
int bit = (n >> 1); // 처음엔 n / 2
while (j >= bit) { // bit 보다 크거나 같은 경우 가장 큰 bit 를 계속 제거
j -= bit;
bit >>= 1;
}
j += bit;
// 여기는 당연히 해당 비트가 없을 것, 켜짐. 결국 j 는 i 의 비트 reverse 한 값이됨
// J --> 100, 010, 110, 001, 101, 011, 111 비트 반전된 1~n 을 따라감
if (i < j) swap(a[i], a[j]); // 상호 적용되므로 두번 적용하지 않음
}
// 미리 사용할 복소수 회전 인자 (roots of unity) 를 저장할 벡터
// roots of unity 란 1의 거듭제곱이 되는 복소수
// 단위 원에서 각도를 동일한 간격으로 나눈 복소수 점
// 근데 n/2 까지만 구하는 이유는 짝수점 홀수점이 나눠져있기 때문에 주파수를 n/2 까지만 사용해도 되기 때문
vector<cpx> roots(n / 2);
double ang = 2 * acos(-1) / n * (inv ? -1 : 1);
for (int i = 0; i < n / 2; i++) {
// wn = cos(2PI / n) + i sin(2PI / n)
// roots[0] = 1 (cos = 1, sin = 0)
// roots[1] = (wn)
// roots[k] = (wn)^k
roots[i] = cpx(cos(ang * i), sin(ang * i));
}
// FFT Cooley-Tukey FFT
// 길이가 i 인 부분배열을 처리 (2, 4, 8, ..n)
for (int i = 2; i <= n; i <<= 1) {
// 길이에 따라 여러번 겹쳐진 상태를 계산
// 다만 짝 홀수번째로 나눠서 계산 될거임
int step = n / i;
// 나눠진 구간을 순회.
// j += i 기 때문에 j 는 구간의 시작점
for (int j = 0; j < n; j += i) {
// 짝 홀수 나눠져있기 때문에 k 를 i/2 만큼씩 사용
for (int k = 0; k < i / 2; k++) {
// (j + 0) ~ (j + k) 짝수부
cpx u = a[j + k];
// (j + 0 + i / 2) ~ (j + k + i / 2) 홀수부
cpx v = a[j + k + i / 2] * roots[step * k];
a[j + k] = u + v;
a[j + k + i / 2] = u - v;
}
}
}
if (inv) for (int i = 0; i < n; i++) a[i] /= n;
}
'개발 > 알고리즘' 카테고리의 다른 글
| Suffix Array 개념 이해 (0) | 2021.01.01 |
|---|---|
| BOJ 11003 최솟값 찾기 (0) | 2020.10.04 |
| golang Fast IO for algorithm (0) | 2020.05.07 |
| Trie 자료구조 (0) | 2019.07.21 |
| Bit Masking (비트 마스킹) (0) | 2019.07.19 |
- Total
- Today
- Yesterday
- C++
- ad skip
- cockroach db
- Obstacle Avoidance
- shared_from_this
- print shared_ptr class member variable
- chrome-extension
- 에러 위치 찾기
- vrpit
- Quest2
- it's called a vrpit
- Reciprocal n-body Collision Avoidance
- Visual Studio
- hole-punching
- SuffixArray
- 잘못된 빨간줄
- 카카오
- boost
- set value
- Golang
- 클래스 맴버 변수 출력하기
- 우리는 vr핏이라고 부릅니다
- vr핏
- 코어 남기기
- 면접
- red underline
- 봄날에 스케치
- mysql
- RVO
- 영상 픽셀화 하기
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |

