티스토리 뷰
원문 링크
https://gamma.cs.unc.edu/ORCA/publications/ORCA.pdf
속도와 위치로 서로 피해서 목표 위치까지 도달하는 것이 목적입니다.
상대방에게 영향을 주는것이 아니고, 주변의 상황을 보고 내 경로를 변경합니다.
위 기술을 적용하여 만들어진 라이브러리가 RVO 인데, 해당 라이브러리를 구현하면 아래처럼 회피하는 움직임을 구현할 수 있습니다.
아래 영상들은 RVO 코드를 사용해서 GameMaker 로 제작해본 데모입니다.
https://www.youtube.com/watch?v=Ax-7CdABpwo
https://www.youtube.com/watch?v=nJaWstq07n4
논문의 개념을 차근차근 알아봅시다.
1. velocity obstacle
A 라는 agent 가 B agent 와 충돌하게 되는 속도를 뜻합니다.
그림으로 표현하자면 아래와 같습니다.

위와 같은 상황일때 A 와 B가 부딪히지 않는 상황을 살펴봅시다.
주황색 위치로 가면 충돌하지 않고, 빨간색 위치로 가면 충돌합니다.
A 와 B의 반지름을 생각해서 충돌이 되는지 판단해야합니다

여기까지 이해가 되셨나요? 논문에 나와있는 내용으로 보면, 아래 그림까지 도달했네요.
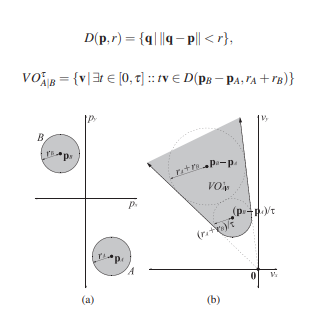
여기서 설명 안된부분은 τ 기호입니다.
τ 는 time window 로 A의 속도에 상수 배 t ( 0 <= t <= τ ) 를 했을때 충돌이 나는지 확인하는 용도로 사용합니다.
상수를 지정하게 되면 피해야 하는 영역을 감지할 타이밍을 지정할수 있겠네요.
위의 VO A|B 는 B 에 대해서 A 가 V 만큼 이동시 충돌이 나는 영역입니다.
VO B|A 는 VO A|B 에 대해서 원점 대칭으로 나오겠죠?
2. Collision Avoiding
만약 A의 속도가 VO A|B 영역에 들어간다면 B 와 충돌이 나겠죠? B 와 충돌이 나지 않게하는 영역을 Collision Avoding 이라 합시다.
앞에 까지는 B의 속도가 0이라고 생각했지만 B가 움직이는 경우도 생각해야합니다.
위에서 그린 VO A|B 영역에 B의 속도(V B)를 Minkowski 합한 영역을 피해야 합니다.
Minkowski 합이 뭐냐면 공간을 합친 점의 집합이라고 생각하면 됩니다. 기호로는 ⊕ 를 사용합니다.
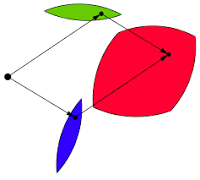
그러면 VO A|B ⊕ V B 영역을 구할 수 있고, 해당 영역에 들어오지 않는 구간은 앞으로 CA A|B 라고 표현할수 있겠죠?
CA A|B 는 A가 B와 충돌하지 않고 움직일수 있는 속도의 집합입니다. 아래 그림에서는 색칠되지 않은 하얀 영역이네요.
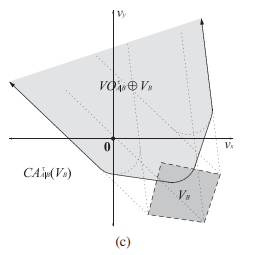
3. ORCA Line
위에서 구한 CA A|B 는 너무나 영역이 넓습니다.
충돌을 피하는 영역 중에서도 내가 가려고하는 목적지에 최대한 가깝게 가는게 좋겠죠?
갈수 있는 여러 속도중 최적화 하여 갈수있는 속도의 집합을 ORCA 라고 합니다
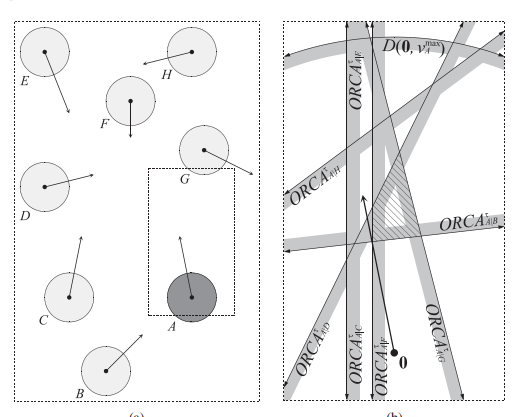
A 와 B 가 아래위치에 있을 때를 기준으로 설명해보겠습니다.
VO 는 A가 가면 안되는 속도로 원점이 A 의 위치라고 생각하면 편합니다.
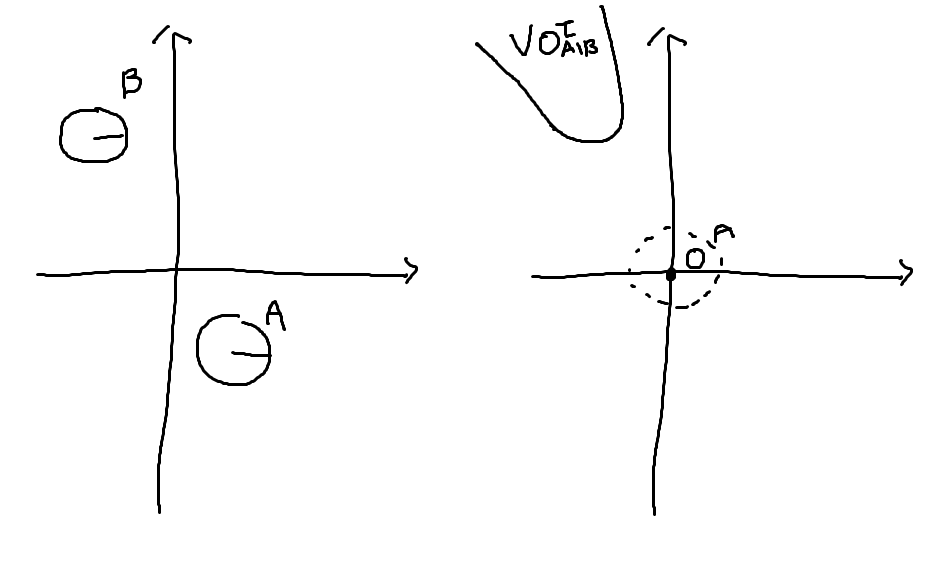
B와 A 각자 속도를 가지고 있을 때, B 에 대한 A의 상대속도를 구할수 있습니다. 벡터 표현상으로는 VA - VB 가 되겠죠. 그러면 B가 멈춰있다고 가정하고 A만 움직인다고 생각할수도 있습니다.
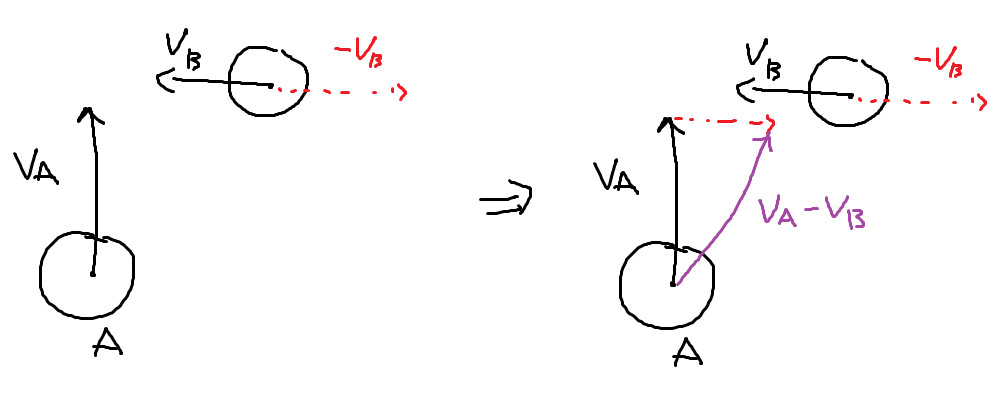
그렇다면 A의 상대 속도가 VO 에 들어가지 않는다면 충돌하지 않겠죠.
아래 사진에서 빨간색은 충돌, 파란색은 충돌하지 않는 상태입니다.
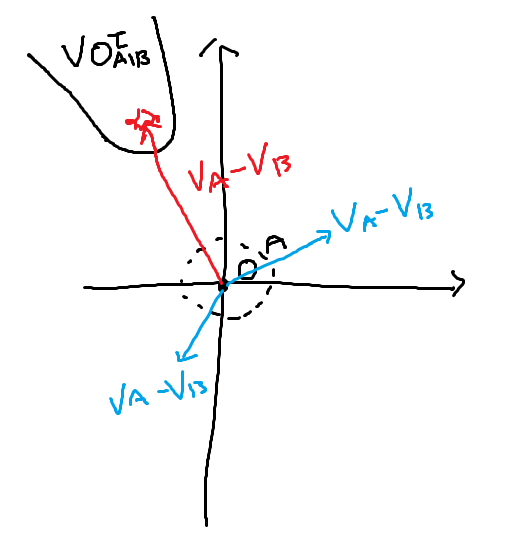
충돌하지 않는 경우는 그냥 둬도 되겠죠. 충돌 했을때 처리입니다.
A의 상대속도가 VO A|B 영역에 들어갔다면 가장 가까운곳으로 나가는 벡터를 찾습니다. 이 벡터는 u 라고 이름 짓습니다.
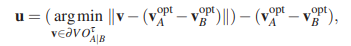
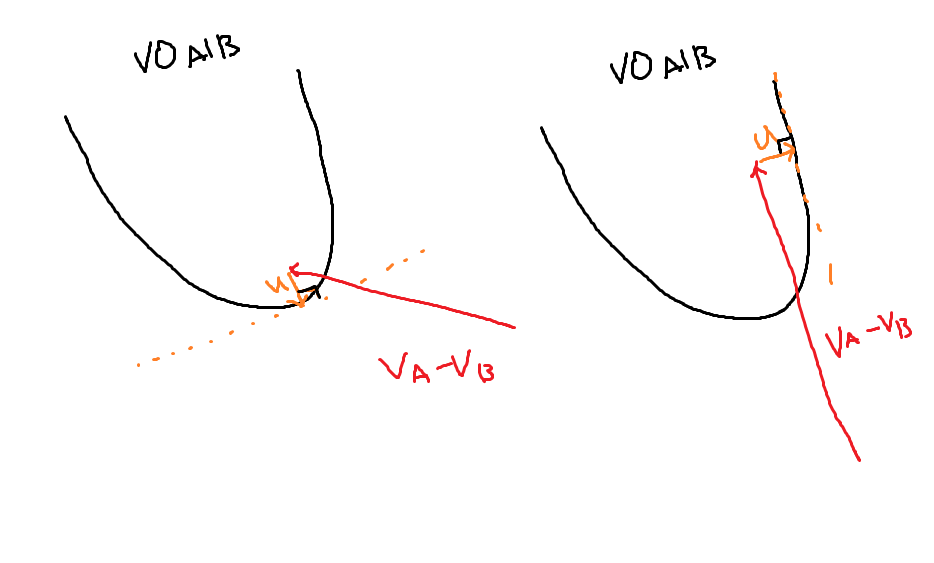
그러면 원래 이동하려고 했던 VA 에 u 만큼을 더한다면 충돌은 일어나지 않겠죠.
하지만 이 논문에서는 상대방도 동일하게 피하는 상황을 가정했기 때문에 실제로는 (1/2) u 만큼만을 사용합니다.
예시를 들어보자면 아래 주황색 벡터를 보면 됩니다.

그러면 논문에서 바라는 ORCA 영역을 구할 수 있게 됩니다. 아래 그림을 봅시다.
u 와 방향이 같은 유닛벡터를 n 이라고 하겠습니다.
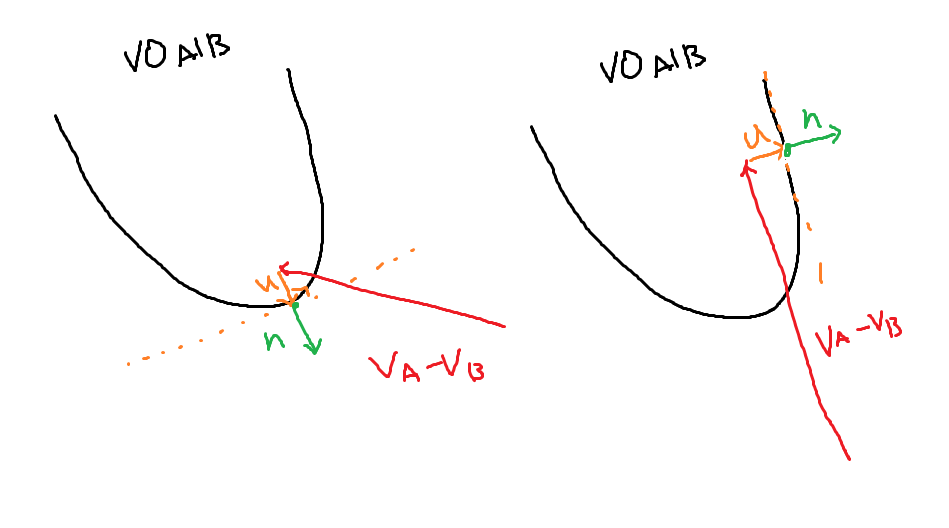
n 벡터와 90도가 넘지 않는 영역에 대해서는 충돌이 나지 않겠죠..
평면을 나누는 직선을 ORCA Line 이라 부르고, 내가 갈수 있는 영역은 half plane ( 한 직선으로 나눠진 평면 ) 으로 표현됩니다.
아래 그림에서 초록색 영역이 ORCA 가 포함하는 구간이고, VO A|B 는 갈수 없는 영역입니다.
그렇다면 분홍색으로 칠한 영역은 뭘까요? 갈 수는 있는 영역이지만, 목적지에 더 빨리 가기 위해서는 초록색 영역으로 가야 하겠죠?
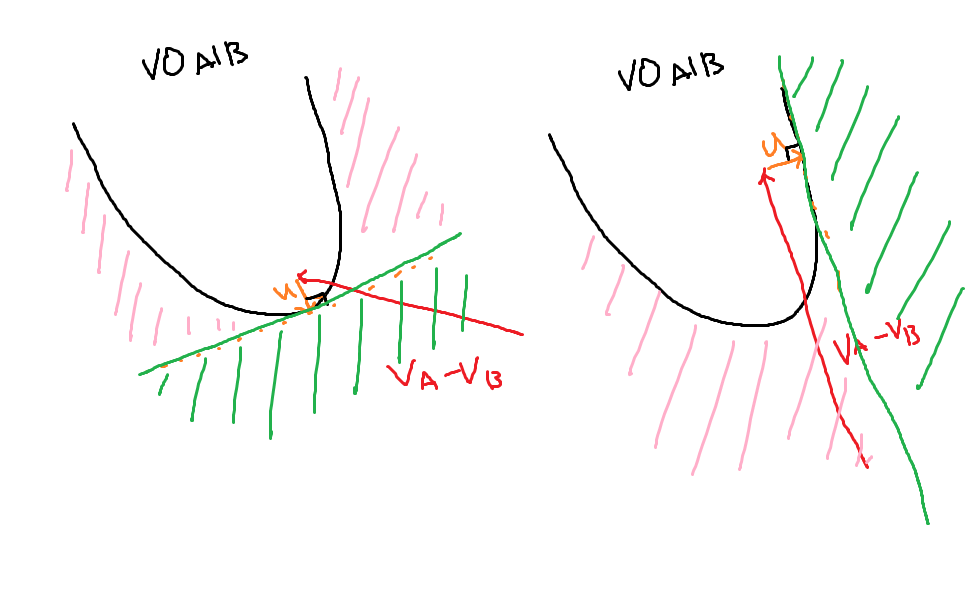
최종적으로는 다음과 같습니다. 위에서 u 의 (1/2) 만 사용한다는건 잊지 않죠?

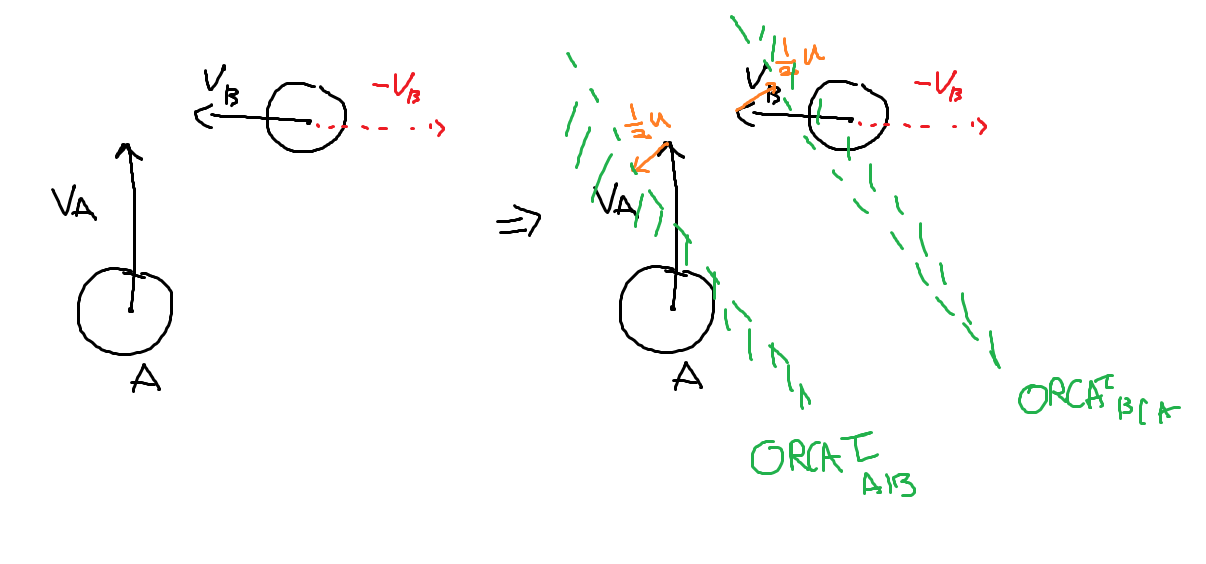
이렇게 내가 이동할수 있는 영역을 찾고, 그 영역안에서 내가 갈수 있는곳을 찾아가면됩니다.
이동 할수 있는 영역을 찾는건 선형 계획법을 사용합니다.
아래 그림의 색칠된 영역을 갈 수 있게 되죠
이상으로 Reciprocal n-body Collision Avoidance 논문에 대해 알아봤습니다.
'개발 > 일상' 카테고리의 다른 글
| mysql 날짜에서 요일 얻어내기 (0) | 2022.10.20 |
|---|---|
| libpng zlib build in linux (centos) (0) | 2022.09.29 |
| visual assist 단축키 등록하기 (0) | 2022.06.14 |
| [git] osx - remote: Invalid username or password. (0) | 2022.06.02 |
| WinSCP 숨김파일 보이기 (0) | 2022.05.06 |
- Total
- Today
- Yesterday
- 봄날에 스케치
- hole-punching
- red underline
- Reciprocal n-body Collision Avoidance
- cockroach db
- SuffixArray
- 클래스 맴버 변수 출력하기
- vrpit
- ad skip
- 면접
- set value
- Visual Studio
- vr핏
- boost
- Quest2
- RVO
- 카카오
- 코어 남기기
- 에러 위치 찾기
- shared_from_this
- 잘못된 빨간줄
- Obstacle Avoidance
- chrome-extension
- mysql
- C++
- it's called a vrpit
- Golang
- print shared_ptr class member variable
- 영상 픽셀화 하기
- 우리는 vr핏이라고 부릅니다
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |

